Geoffrey Hinton著 "The Forward-Forwardアルゴリズム" まとめ

The Forward-Forward Algorithm : Some Preliminary Investigations (加筆修正版) Geoffrey Hinton 1

⾃⼰紹介 ROCMan • 来年春から新卒GPUエンジニアの修士2年生 • 深層学習とGPUプログラミングがちょっとわかる • たまに深層学習系の論文読んでスライドにまとめてます twitter垢： https://twitter.com/ROCmannn 2

• https://twitter.com/ROCmannn

はじめに 本スライドは、 Geoffrey Hinton著： “The Forward-Forward Algorithm : Some Preliminary Investigations” の内容を要約した物です ※注意事項 元論文は説明の省略が激しく、 要所で私の想像による補完がなされています あくまで解釈の一つと捉えてください🙏 3

⽬次 • 概要 • 背景 • Forward-Forward(FF) アルゴリズム • FF for 教師なし学習 • FF for 教師あり学習 • RNN-likeにFFを性能改善 • 実験 • FFが秘めるポテンシャル • まとめ 4

概要 5

概要 • 2種類のforwardだけで勾配計算する新たな学習の枠組みを提案 • “正データ”と“負データ”を用いて、以下のようにlayer毎に勾配計算 • “正データ”でforwardを回した時は、中間値ベクトルのノルムを最大化 • “負データ”でforwardを回した時は、中間値ベクトルのノルムを最小化 6

背景 7

背景 現在の深層学習はbackpropが主流 rabbit kawauso cat 🤔だが、生物の脳はback propなんてしてるの？ Ø脳に習うなら、forwardだけで学習を完結させるのが筋！ Øメモリ効率も良くなるしね 8

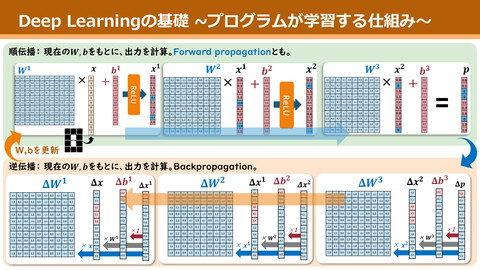
そもそも何故backpropが必要だった︖ 出力 正解label 𝑧 = 𝑥𝑊 𝜕𝐿 𝜕𝐿 ∴ =𝑥 𝜕𝑊 𝜕𝑧 Ø𝑊の勾配計算には, 次の中間値の勾配が要る L正解から直接feedbackを 受けられるのは,最終層の出力だけ Øだからこそ, chain則で feed backを前方の中間値にリレー 0.1 1 rabbit 0.4 0 cat 0.5 0 kawauso 出力 正解label 0.1 1 rabbit 0.4 0 cat 0.5 0 kawauso 出力 正解label 0.1 1 rabbit 0.4 0 cat 0.5 0 kawauso 出力 正解label 0.1 1 rabbit 0.4 0 cat 0.5 0 9 kawauso

勾配リレーしたくない… 勾配リレー無しでできない？ Ø各中間値に直接, 正解のfeed back を与える他ない 直接微分を計算すればできるけど… Øメモリ増えて本末転倒 𝑦 = (𝑥!𝑊!)W" 𝜕𝐿 𝜕𝐿 ∴ = 𝑥!𝑊" 𝜕𝑊! 𝜕𝑦 根本から考え方を変えましょう 正解 ? rabbit ? cat ? kawauso ? 10

Forward-Forward Algo. 11

Forward-Forward(FF) Algorithm • どんなtaskも,入力を正か負の2値に分類するtaskに強引に変換 • 各入力をNNに流し, 以下の方針で重みを手前から1層ずつ学習 • 正な入力：各層の中間値ベクトルのノルムを最大化 • 負な入力：ノルムを最小化 Øこの2種類のForward更新が名前の由来 • layer normが, 各層でノルムだけはリセットする 入 力 Linear 中 間 値 Layer Norm Linear 中 間 値 Ø活性or不活性という神経細胞ライクな反応になる 12

教師なし学習的な使い⽅ MNISTの手書き数字判別モデルを作る • 画像から表現ベクトルに変換するNN + それを元に分類する全結合層 • この前半のNNを教師なしFFで作る Embedding NN 表 現 ベ ク ト ル Decoding Linear 0 0 0 0 0 1 0 0 0 Letʼs FF! 13

教師なし学習的な使い⽅ 正データ … 普通の手書き数字画像 負データ … 2種の数字を合成した変な図形 これらを用いてFFアルゴでNNを学習 Ø入力画像から得られる各中間値を結合し, 表現ベクトルと見なす FFで学習 labelで普通に学習 Linear 中 間 値 Layer Norm Linear 中 間 値 中 間 値 中 間 値 Decoding Linear 14 0 0 0 0 0 1 0 0 0

教師なし学習での性能を実験 • 2000次元の中間値x4のNNを100epoch学習 • 最後の3つの中間値を用いて分類器を学習 ØMNISTでのtest error率：1.37% Linear 中 間 値 0 0 0 0 0 1 0 0 0 Layer Norm Decoding Linear 15

ちょっと性能改善させてみたよ Linear層をlocal receptive fieldに換えてみた Øtest error率が1.16%まで減少 cf. ) Local Receptive Field Ø重みを贅沢に使う畳み込み層 • filter内で重みを使い回さず,1pixelの計算毎に個別の重みを用意 畳み込み層：同じ重みで全pixel作る LRF：pixel毎に重みを変える 16

教師あり学習的な使い⽅ MNISTの手書き数字判別モデルを作る • 画像から分類まで行うNNをFFで作る 出力 正解label 0.1 1 0.4 0 0.5 0 • backpropのようにlabel情報を出力層から入れられない labelのone-hot Ø入力画像に埋め込む 正データ • 画像の数字とlabel情報が一致 負データ • 画像の数字とlabel情報が不一致 17

教師あり学習での性能 一つの画像に対して、label0~9を埋めた10枚をそれぞれ推論 中間値たちのノルムが最大だったlabelを推論結果とする • 2000次元の中間値x4のNNを60epoch学習 Øtest error率：1.36% Øbackpropは20epochくらいで同じくらいの精度に到達 large? small? ・・・ large? small? large? small? large? small? Linear 中 間 値 Layer Norm 18

FFの性能改善 19

ここまでのFF⽅式の問題点 • 再掲）入力をNNに流し, 以下の方針で重みを手前から1層ずつ学習 • 正な入力：各層の中間値ベクトルのノルムを最大化 • 負な入力：ノルムを最小化 Ø前方のlayerの学習が終わってから次のlayerの学習が始まる ØL後方のlayerは前方の学習に関与できない Øbackpropと比べて性能面で明確に劣る点 入 力 Linear 中 間 値 Layer Norm Linear 中 間 値 20

RNN-likeに解決 モデル構造をRNNっぽく変更 • 同じ画像(とlabelのone-hot)を 動画のように複数(10くらい)回入力 • 中数回の中間値ノルムの大きさを利用 ↓ " " 𝑥!"#$ = 0.7𝑥!" + 0.3(𝑊!#$ 𝑥!#$ + 𝑊!↑ 𝑥!'$ ) (※ 𝑥!"#$ , 𝑥!" はlayer norm前の値） で中間値を更新 ØJ後方の情報が前方の更新を使用 (メモリ消費増えてる気がする…) 𝑥!" 𝑥!"#$ " 𝑥!%$ t t+1 時間軸 21

補助図（になればいいが） ↓ " " • 𝑥!"#$ = 0.7𝑥!" + 0.3(𝑊!#$ 𝑥!#$ + 𝑊!↑ 𝑥!'$ ) 入 力 Linear 中 間 値 Layer Norm Linear 中 間 値 Layer Norm Linear 22

RNN-like ver.での正/負データ • 正データ…画像と正しいlabel • 負データ…画像と誤ったlabel※ Ø画像を1回forwardに通し、そこから各 classの確率分布を計算 Øそれに応じて、どの誤labelのデータを 何個ずつ作るか決める 𝑥!" 𝑥!"#$ " 𝑥!%$ 時間軸 23

RNN-like ver. on MNIST • 2000次元の中間値x2(or3)のNNをMNISTで60epochs学習 • forwardを“8回 / label” 回して、3~5回目での中間値のノルム の平均が最も大きかったlabelを推論結果とした Øtest error率：1.31% Ø通常の教師ありver.より0.05%の改善 24

RNN-like ver. on CIFAR-10 • 32x32x3次元の中間値(特徴map)x2(or3)のNN Ø特徴mapの1要素は、以下の2つのreceptive fieldから計算 • 前層の11x11x3の領域 • 後層の11x11x3の領域（最終層だけは、labelのone-hotベクトル） • 正データの中間値ノルムを小さく、負を大きく学習するver.(min ssq)も 実験 • forwardを“10回 / label” 回して、4~6回目での中間値のノルムの平均 が最も大き（or 小さ）かったlabelを推論結果とした Ø4~6回目で測った時が最も高精度だったらしい • 画像だけを1回forwardに通した際の中間値に、 別途linear+softmaxを連結、学習するone-pass ver. (最初の教師なしと同じ)も実験 25

RNN-like ver. on CIFAR-10 実験結果 Lbackpropより僅かに精度は悪い Øbackpropは完全に過学習 Ø学習速度もbackpropが速いらしい JちゃんとRNN-likeにやるFFの方が、 one-pass FFより精度が良い 26

FF on 次⽂字予測 • 前10文字から次の文字を予測するtask • イソップ寓話内の100文字のstring x 248 のdatasetで学習 • 2000次元の中間値x3のNN • 中間値にlinear+softmax適用で次文字決定 • 負dataは以下の2パターンで実験 A) datasetの最初の10文字から、後続全てに対 してモデルが予測したstringから10文字抽出 B) 9文字はdatasetの実data、last1文字はモデ ルの予測文字 27

FF on 次⽂字予測 実験結果 縦軸はperplexity。低いほど良い 青線：最後のlinear+softmaxだけ学習 赤線：正dataだけで学習後,負dataだけ で学習（負data Aを使用） 黒線：正,負data1つずつの勾配を計算 その和で重み更新（Bを使用） J次文字予測もできる J正負交互に学習する必要は無いらしい 28

Forward-Forwardの ポテンシャル 29

FFの最⼤の⻑所︓layer間の独⽴性 FFは,層毎に中間値ノルムを最大(小)化するように重みを更新 Øある層の重みを更新しても, 出力するN中間値が変わらない*性質 *重み更新時と 入力が同じ時のみ übackprop方式より, layer間の独立性が高い Linear 中 間 値 Layer Norm N 中 間 値 Linear 中 間 値 Layer Norm N 中 間 値 Layer Norm N 中 間 値 前方のlayerの 重みを更新しても, 後半は影響を受けない ここが同じ値に！ Linear 中 間 値 Layer Norm N 中 間 値 Linear 中 間 値 30

前ページの証明 𝑥: 入力, 𝑊: Linear層の重み, 𝑦: 中間値 𝑥 𝑦 * 𝑊 中間値ノルムを最小化: 𝐿𝑜𝑠𝑠 = y 𝜕𝐿 𝜕𝑦 𝜕𝐿 = 𝜕𝑊 𝜕𝑊 𝜕𝑦 = 𝑥 # ⋅ 2𝑦 = 2𝑥 # 𝑦 ! = yy " 𝜕𝐿 𝑥 𝑊+ = 𝑥𝑊 + 𝑥 ⋅ 2𝑥 # 𝑦 𝜕𝑊 = 𝑦 + 2𝑥𝑥 # 𝑦 = 1 + 2 𝑥 ! 𝑦 ☜重み更新前の中間値yの定数(1 + 2 𝑥 ! )倍 これはLayer Normで正規化されると同じ値に！ 31

layer間の独⽴性 FFは, backprop式より, layer間の独立性が高い Øblack boxな変換を途中に差し込んでも学習ができる Linear 中 間 値 Layer Norm N 中 間 値 Oracle Layer Norm N 中 間 値 Linear 中 間 値 32

⻑所をシンプルに使うなら “layer間にblack boxな変換を入れても学習できる“ Øblack boxとして、普通のNNを入れてみる(blackじゃないけど) Øblack boxとそれ以外のlayerで学習の速度を変えるなどが可能 使用例：continuous learning • 中間のlayersはゆっくり学習 Ødomainの長期的な変化に追従 • 周りのlayersは高速に学習 Ødomainの短期的な変化に追従 入 力 fast adapt NN slow adapt NN fast adapt NN 33

mortalなソフトの可能性 近年の計算科学は, ハードとソフトの分離を目指して発展 ØJハードが故障しても, ソフトは他のハードですぐ実行できる Øソフトのimmortality(不死身化)による発展 不死身化を捨て, 特定の超低消費電力ハード（例えば生物細胞） に依存したソフトを作れたら？ ØLハードが一度壊れれば、またソフトも作り直し ØJ大規模計算を劇的な低消費電力で行える可能性 34

FFによるmortalな深層学習の可能性 FFには、これを実現するポテンシャルがある！ Ølayer間にblack boxとしてどんな物（生物細胞）も入れられる Ø活性or不活性という細胞likeな学習をさせるため,親和性も◎ Ø超低消費電力NNを実現する唯一の方法！！！ Linear 中 間 値 Layer Norm N 中 間 値 Layer Norm N 中 間 値 Linear 中 間 値 35

まとめ 36

Forward-Forwardアルゴリズムまとめ • 2種類のforwardだけで勾配計算する新たな学習の枠組みを提案 Ø“正データ”と“負データ”を元に、layerごとに勾配計算 • backpropには未だ性能は劣るものの, 様々なtaskで性能発揮 • ネットワークの内部にblack boxを持っても学習ができる Ø生物細胞等, 超低消費電力なハードを取り込める可能性 Linear 中 間 値 Layer Norm N 中 間 値 Layer Norm N 中 間 値 Linear 中 間 値 37

FFはアナログ回路と相性が良い︖ らしい。 38

読了感謝︕ twitter垢： https://twitter.com/ROCmannn ↑少しでもわかりやすいと思ってくれたらフォローお願いします 39

• https://twitter.com/ROCmannn